AbeLie matematikk

Tvillingtall

Herons metode

Å regne ut arealet av en trekant der de tre sidene er gitt er ikke så liketil. Man kan resonere seg frem til det, men det kan lett bli komplisert. Heron fra Alexandria utviklet en metode der man går inn i en prosess som gir resultatet på relativt greitt sett. Heron går ut fra et eksempel: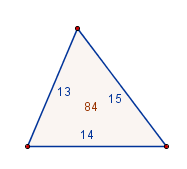
En trekant er gitt med sider 13, 14 og 15. Vi skal finne arealet av trekanten, og det gjør vi ved først å finne fire nye tall ut fra de tre sidene. Vi legger først sammen de tre tallene og deler på to, og får tallet 21, og da har vi det første tallet. Fra dette tallet trekker vi fra hver av de tre sidene, og får tre nye tall som er 6, 7 og 8. De fire tallene vi her har fått multpliserer vi så med hverandre og får 7056. Dette tallet tar vi kvadratroten av og får 84, som er arealet til trekanten.
Dette er et eksempel på å danne det vi kaller tvillingkvadruppel.

Tvillingtallene

I flere områder av matematikken kommer et tallmønster som vi kaller tvillingkvadrupler til syne. Dette er to grupper tall med fire tall i hver gruppe der de to gruppene har flere identiske egenskaper. De fire tallene i en gruppe fremkomer av de fire tallene i den andre gruppen. Man kan blandt annet anvende tallene til å finne arealet av en trekant og av en firkant innskrevet i en sirkel. Denne metoden for å finne areal kalles Herons metode etter matematikeren Heron fra Aleksandria.

En kortere benevnelse på tvillingvadrupler er tvillingtall.

Vi skal først se på tvillingtallene fremkommer eksempelvis, og senere se hvordan det kan forstås algebraisk.

Fremkomst av tvillingtall

  1. Velg fire tall fritt men slik at summen av dem er delelig på 2, og der det ikke er like stort mellomrom mellom de to minste og de to største tallene. Kall tallene $a_1$, $a_2$, $a_3$ og $a_4$.
  2. Finn summen av tallene.
  3. Finn den halve summen og kall denne for s.
  4. Trekk hvert av tallene a fra summen (et ad gangen) slik at du får fire nye tall. Kall disse $b_1$, $b_2$, $b_3$ og $b_4$ der $b_1$ er det tallet du får når du trekker $a_1$ fra halvsummen.
  5. Finn summen av de fire nye tallene. Hva ser du.
  6. Finn kvadratsummen av de fire første tallene, og så kvadratsummen av de fire neste tallene. Hva ser du? (Kvadratsum vil si å gange tallene med seg selv, og så legge sammen de fire resultatene.)
  7. Finn kryssproduktene av hver kvadruppel.( $a_1\cdot a_2+a_3\cdot a_4$) og ( $b_1\cdot b_2+b_3\cdot b_4$)(Vi kan skifte om på indeksene her)
  8. Gjenta prosessen med fire nye tall.

Tvillingtall ut fra kuben

Vi studerer en terning. Den har seks sideflater og åtte hjørner. De åtte hjørnene kan deles inn i to grupper, der fire høre med til hvert tetraeder. Det er tre tilstøtende flater til hvert hjørne.

Arealet av en innskrevet firkant

For å finne arealet av en innskrevet firkant der de fire sidene er gitt finner man tvilligtallene til de fire tallene, tar produktet av disse, og så kvadratroten av resultatet. $$F = \sqrt{b_1 \cdot b_2 \cdot b_3 \cdot b_4}$$

Arealet av en trekant

Arealet av en trekant finner man på tilsvarende måte fordi en trekant kan ses på som en innskrevet firkant der den ene siden er 0.

Algebraisk fremstilling av tvillingtall

Ved eksemplene har vi sett at tvillingtallene har mange egenskaper som ser ut til å gjelde for alle tall. Ved å sette inn algebraiske utrykk for dem kan vi vise at forholdene gjelder generelt.

Vi velger en fremstilling av tallene som gjør dette enklere.
Vi setter $a_1 = a+c$, $a_2 = a-c$, $a_1 = b+d$ og $a_1 = b-d$.

  1. Hva blir halvsummen av disse fire utrykkene?
  2. Finn utrykket for de fire tvillingtallene $b_1, b_2, b_3$ og $b_4$
  3. Finn $\sum_{i=1}^4 a_i^2$ og $\sum_{i=1}^4 b_i^2$
  4. Regn ut $a_1\cdot a_2+ a_3\cdot a_4$ og $b_1 \cdot b_2+ b_3 \cdot b_4$.