AbeLie matematikk

Ptolemaios heltall

---

---

Det er vel kjent at vi kan finne heltallige verdier for pytagoras trekanter. Vi kan også finne såkalte Heronske trekanter; det er trekanter der sidenes lengder er integre, der arealet også utrykkes med et helt tall. Vi skal i denne sammenheng se på en nært beslektet problemstilling, det vi kan kalle Ptolemaiske firkanter. Disse er firkanter innskrevet i en sirkel der både sidene og diagonalene er hele tall.

Når vi kaller firkantne "Ptolemaiske firkanter" så går dette tilbake til Claudius Ptolemaios som levde i Aleksandria. Den kjente setningen som bærer hans navn kan anvendes på like måter.

Disse er behandlet i ulike sammenhenger, men da som regel med utgangspunkt i heronske trekanter, d.v.s at da blir arealet også heltallig. Vi skal se på en annen vei der det fremkommer at den heronske varianten er et spesialtilfelle av en mer generell form.

Når sidene er gitt ved de frie varible $u$, $v$ og $w$ kan vi få heltallige strukturer.\begin{eqnarray*} % \nonumber to remove numbering (before each equation) a &=& (v + u w)(w + u v) \\ b &=& (w + u v) (u + v w) \\ e &=& (u + v w)(v + u w) \\ c &=& (1 + u) (w - v)(u + v w) \\ d &=& (1 + v) (u - w)(v + u w) \\ f &=& (1 + w) (u - v)(w + u v) \end{eqnarray*}

Denne fremstilling er brukt i appletten.

---

Ptolemaios setninger

For firkanter innskrevet i en sirkel gjelder ptolemaios setning:

Setning: Gitt en firkant ABCD innskrevet i en sirkel. Da vil summen av produktene av motstående sider være lik produktet av diagonalene: $$AB\cdot CD+ AD \cdot BC = AC \cdot BD$$

Denne setningen er også kriteriet for at de fire punktene skal ligge på en sirkel.

Setter vi nå $\{AB,AC,AD,BC,BD,CD\} = \{a,e,d,b,f,c\}$ blir utrykket enklere:$$ac+bd=ef$$

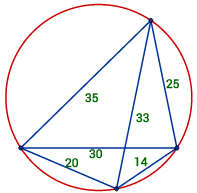
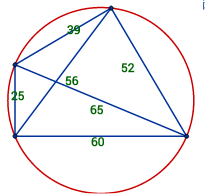
For denne ligningen kan vi enkelt finne rasjonale løsninger. Har vi gitt fem av størrelsene, vil den sjette være rasjonalt gitt av disse. Nå gjelder imidlertid også en annen setning for en innskrevet firkant. Danner vi produktene av sidene i de fire trekantene i firkanten, vil summen av produktene til motstående trekanter være like: $$ade+bce=abf+cdf$$

Disse to relasjonene er uavhengige av hverandre, og vi kan dermed finne to ukjente sider når fire størrelser er gitt. Hvis vi for eksempel kjenner de fire sidene, kan vi finne de to diagonalen ved å løse de to ligningene simultant. Vi får da kvadratiske utrykk for diagonalene: $$e=\sqrt{\frac{(a c+b d)(a b+c d}{a d+ b c}}$$ Derav ser vi at fire rasjonale sider ikke umiddletbart gir rasjonale diagonaler.

Tallteoretisk

Vår oppgave er altså å finne rasjonale tall som tilfredstiller begge ligningene $$I\; ac+bd=ef$$ $$II\;ade+bce=abf+cdf$$

I en artikkel av i Forum geometricorum blir dette sett rent geoemtrisk. Vi skal se på en rent algebraisk tilnærming, men de ulike trinnene skal også anskues geometrisk.

Utrykkene over bringes på en symmetrisk form ved å finne halve summen og differansen av motstående sider, og urykke lengdene av sidene ved disse: $$ a = p_1+q_1,\;c =p_1-q_1,$$ $$b= p_2+q_2 ,\;d = p_2-q_2,$$ $$e=p_3+q_3,\;f =p_3-q_3$$ Da vil lignignene gå over til $$p_1^2+p_2^2+p_3^2=q_1^2+q_2^2+q_3^2$$ $$p_1\:p_2\:p_3=q_1\:q_2\:q_3$$ Problemstillingen har dermed gått over til å finne to grupper av tre rasjonale tall der både produktet og kvadratsummen blir den samme. Geometrisk er dette å finne to ulike prismer der diagonalene og volumene er like store utrykkt ved rasjonale tall.

Disse to ligningene kan videre gjøres om til en ligning ved å sette $$p_1=x_2\;y_3,\;p_2=x_3\;y_1,\;p_3=x_1\;y_2$$ $$q_1=x_3\;y_2,\;q_2=x_1\;y_3,\;q_3=x_2\;y_1$$

Her er jo produktene identiske fordi alle faktorene kommer i begge utrykkene. Dermed får vi bare en ligning tilbake: $$(x_1y_2)^2+(x_2y_3)^2+(x_3y_1)^2=(x_2y_1)^2+(x_3y_2)^2+(x_1y_3)^2$$

Determinantform

Sammenhengen her kan settes på determinantform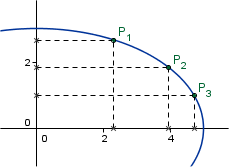 Dette utrykket er kriteriet for at tre punkter skal ligge på samme sentrale kjeglesnitt. Vi ser dette ved å la det ene punktet være fritt, og de andre to faste. Vi får da: $$x^2 y_2^2+x_2^2 y_3^2+x_3^2 y^2=x_2^2 y^2+x_3^2 y_2^2+x y_3^2$$ som kan omskrives til $$\frac{x^2}{\frac{x_3^2 y_2^2-x_2^2 y_3^2}{y_2^2-y_3^2}}+\frac{y^2}{\frac{x_3^2 y_2^2-x_2^2 y_3^2}{x_3^2-y_2^2}}=1$$som er normalformen til et sentralt kjeglesnitt. Det er gitt ved formen \begin{equation}\label{kjegle} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \end{equation} Som kjent kan vi finne uttallige rasjonale punkter på et kjeglesnitt når vi kjenner ett. Vi kan derfor finne løsninger på vårt problem ved å finne kjeglesnitt gjennom et kjent punkt, og så finne to andre punkter på kjeglesnittet.
Vi skal imidlertid gå en litt annen vei for å finne direkte utrykk. Vi fremstiller nå $x_i$ og $y_i$ ved variablene $a_j$ og $b_j$ ved
Utregnet, forkortet og dividert med $a_1\;a_2\;a_3\;b_1\;b_2\;b_3$ gir dette $$\frac{1}{a_1\;b_2}+\frac{1}{a_2\;b_3}+\frac{1}{a_3\;b_1}=\frac{1}{a_2\;b_1}+\frac{1}{a_3\;b_2}+\frac{1}{a_1\;b_3}$$ På determinatform blir denne $$ \left| \begin{array}{ccc} 1 & 1 & 1 \\ \frac{1}{a_1} &\frac{1}{a_2} & \frac{1}{a_3} \\ \frac{1}{b_1} & \frac{1}{b_2} & \frac{1}{b_3} \\ \end{array} \right|=0 $$ Dette er betingelsen for at tre linjer går gjennom samme punkt. Når $a_i$ og $b_i$ er punkter på henholdsvis x-aksen og y-aksen, vil linjene $l_i$ gå gjennom et felles punkt.
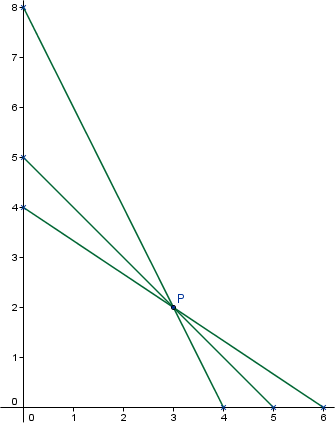
Vi har dermed ført til en lineær problemstillingen, og vi kan finne rasjonale løsninger direkte. Linjer gjennom punktet $x_0$ og $y_0$ er gitt ved \begin{equation}\label{linjer} \frac{x_0}{x}+\frac{y_0}{y}=1 \end{equation} Gitt tre $x$ verdier kan vi finne tre $y$ verdier, og fra disse finner vi rasjonale tall for Ptolemaioskonfigurasjonen. Vi skal nå finne eksplisitte algebraiske utrykk. Da er det er nok å finne linjer som går gjennom punktet (1;1) i koordinatsystemet. Vi skal senere se at dette gir en fullstendig løsning av problemet. Hvis en linje som går gjennom dette punktet skjærer x-aksen i $1+x$, da vil den skjære y-aksen i $1+\frac{1}{x}$. Vi setter da at tre linjer skjærer x-aksen i punktene $1+u,\;1+v$ og $1+w$. Disse vil da skjære y-aksen i punktene $1+\frac{1}{u},\;1+\frac{1}{v}$ og $1+\frac{1}{w}$, og determinanten blir null

\begin{equation} \left| \begin{array}{ccc} 1 & 1 & 1 \\ \frac{1}{1+u} & \frac{1}{1+v }& \frac{1}{1+w}\\ \frac{1}{ 1+\frac{1}{u}} & \frac{1}{1+\frac{1}{v}} & \frac{1}{1+\frac{1}{w}} \\ \end{array} \right|=0 \end{equation} Vi kan nå gå nedover igjen og utrykke de andre variable ved disse frie variable.

Tre rasjonale punkter på samme kjeglesnitt er dermed gitt ved \begin{equation}\label{det3} \left| \begin{array}{ccc} 1 & 1 & 1 \\ 1-u+v+w & 1+u-v+w& 1+u+v-w\\ 1-\frac{1}{u}+\frac{1}{v}+\frac{1}{w}& 1+\frac{1}{u}-\frac{1}{v}+\frac{1}{w}& 1+\frac{1}{u}+\frac{1}{v}-\frac{1}{w}\\ \end{array} \right|=0 \end{equation} For å få heltallsløsninger multipliserer vi den nederste raden med $u\;v\;w$. Det gir for $p$ og $q$. \begin{eqnarray} % \nonumber to remove numbering (before each equation) \nonumber p_1 &=& (1 + u - v + w) (-u v + u w + v w + u v w) \\ \nonumber p_2 &=&(1 + u + v - w) (u v + u w - v w + u v w)\\ \nonumber p_3 &=& (1 - u + v + w) (u v - u w + v w + u v w) \\ \nonumber q_1 &=& (1 + u + v - w) (u v - u w + v w + u v w) \\ \nonumber q_2 &=& (1 + u - v + w) (u v + u w - v w + u v w) \\ q_3 &=& (1 - u + v + w) (-u v + u w + v w + u v w) \end{eqnarray} Setter vi $s=1+u+v+w$ og $t=u v w+u v +u w+v w$ fremkommer enklere utrykk: \begin{eqnarray} % \nonumber to remove numbering (before each equation) \nonumber p_1 &=& (s-v) (t-uv) \\ \nonumber p_2 &=&(s-w) (t-vw)\\ \nonumber p_3 &=& (s-u) (t-uw) \\ \nonumber q_1 &=& (s-w) (t-uw) \\ \nonumber q_2 &=& (s-v) (t-vw) \\ q_3 &=& (s-u) (t-uv) \end{eqnarray} Vi utrykte opprinnelig sidene ved $p$ og $q$. Går vi nå den andre veien blir sidene gitt ved: \begin{eqnarray*} % \nonumber to remove numbering (before each equation) a &=& (v + u w)(w + u v) \\ b &=& (w + u v) (u + v w) \\ e &=& (u + v w)(v + u w) \\ c &=& (1 + u) (w - v)(u + v w) \\ d &=& (1 + v) (u - w)(v + u w) \\ f &=& (1 + w) (u - v)(w + u v) \end{eqnarray*}

Heronsk

Det viser seg at selv om vi har en rasjonal Ptolemaioskonfigurasjon, er den ikke nødvendigvis Heronsk; arealet trenger ikke være rasjonalt selv om siden er det. Men det er ikke store modifikasjoner som skal til for å oppfylle et slikt krav i tillegg. Vi regner ut arelatet av firkanten ved Bramaputras formel $$F=\sqrt{(s-a)(s-b)(s-c)(s-d)}$$ der $s=(a+b+c+d)/2$ og får \begin{equation}\label{areal} F=\sqrt{16 u v (-u + v)^2 (1 + u + v - w)^2 w (1 + w)^2 (-u v + u w + v w + u v w)^2} \end{equation} \begin{eqnarray} % \nonumber to remove numbering (before each equation) F &=& \sqrt{16 u v (-u + v)^2 (1 + u + v - w)^2 w (1 + w)^2 (-u v + u w + v w + u v w)^2} \\ \; &=& 4(v - v)(1 + w)(-u v + u w + v w + u v w)(1 + u + v - w)\sqrt{u v w} \end{eqnarray} Vi ser at de fleste ledd er kvadratiske, mens $uvw$ kan bli irrasjonalt. Ved å sette ${u,\;v,\;w}={k m,\;m n,\; n k}$ blir produktet et utrykk med kvadrater, og vi kan trekke kvadratroten. Utrykkenen for sidene blir nå \begin{eqnarray*} % \nonumber to remove numbering (before each equation) a &=& n (1 + k^2) (1 + m^2) \\ b &=& k (1 + m^2) (1 + n^2) \\ e &=& m (1 + k^2) (1 + n^2) \\ c &=& (k - m) (1 + k m) (1 + n^2) \\ d &=& (m - n) (1 + m n)(1 + k^2) \\ f &=& (k - n) (1 + k n)(1 + m^2) \end{eqnarray*} Arealet blir da \begin{equation} F= 4 k^2 l^3 m ^2 (1 + k m) (k - m) (1 + k l - k m + l m) (k - l + m + k l m) \end{equation} Spesielt enkelt blir uttrykket for radien til den omskrevne sirkelen ved denne fremstillingen. \begin{equation}\label{sirkel} R=(1+k^2)(1+m^2)(1+n^2) \end{equation}

Omvending

Løsningen er fullstendig fordi vi finner tilbake til $u,\;v$ og $w$ ved $p$ og $q$. Løsningen er gitt ved \begin{eqnarray}\label{omvend} % \nonumber to remove numbering (before each equation) \nonumber u &=& \frac{p_2 p_3 (p_1-q_2) (p_1+q_3)}{q_2 q_3(p_2-q_1) (p_3+q_1) }\\ \nonumber v &=&\frac{p_1 p_3 (p_2+q_1) (p_2-q_3)}{q_1 q_3(p_3-q_2) (p_1+q_2)} \\ w &=& \frac{p_1 p_2 (p_3-q_1) (p_3+q_2)}{q_1 q_2 (p_1-q_3) (p_2+q_3)} \end{eqnarray} For å komme til dette starter vi ikke direkte med sidene i Ptolemaiosfirkanten, men overfører disse til $p$ og $q$. Vi finner fire ligninger som forhold mellom $p$ og $q$. \begin{eqnarray} % \nonumber to remove numbering (before each equation) \nonumber I\;\; \frac{p_1}{q_2} &=& \frac{1+u-v+w}{1-u+v+w} \\ \nonumber II\;\; \frac{p_2}{q_3} &=& \frac{1+u+v-w}{1+u-v+w} \\ \nonumber III\;\; \frac{p_2}{q_1} &=& \frac{u v+u w-v w+u v w}{u v-u w+v w+u v w} \\ IV\;\; \frac{p_3}{q_2} &=& \frac{u v-u w+v w+u v w}{-u v+u w+v w+u v w} \end{eqnarray} Vi løser ligningene I og II simultant med hensyn på $u$ og $v$, og får dem da utrykkt ved $p_i$, $q_j$ og $w$. Vi får da for $u$ \begin{equation}\label{lignignU} u=\frac{p_1 p_2 + q_1 q_2-p_1 p_2 w - p_1 q_3 w}{(p_1+q_2)q_3} \end{equation} Vi løser så ligningene III og IV på samme vis og får et nytt utrykk for $u$ \begin{equation}\label{ligningII} u=\frac{p_3(p_2 + q_1)w}{p_3 q_1 + q_1 q_3 - p_2 p_3 w + q_1 q_3 w} \end{equation} Vi har dermed to utrykk for $w$ som er linært uavhengige, og når vi løser disse med hensyn på $w$ har vi \begin{equation}\label{utrykkW} w=\frac{q_1(p_1 + q_3)(p_1 p_2-q_2 q_3)}{p_1(p_2 + q_3)(p_2 p_3 - q_1 q_3)} \end{equation} Setter vi til slutt $q_2q_3=\frac{p_1 p_2 p_3}{q_1}$ og $q_1q_3=\frac{p_1 p_2 p_3}{q_2}$ går utrykket over til det vi skulle vise. Til enhver Ptolemaios kan vi nå finne genererende elementer, og fremstillingen er derfor fullstendig. En skaleringsfaktor kommer i tillegg.

Claudius Ptolemaios