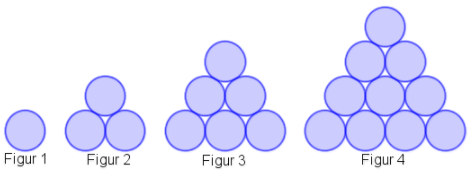
 De fremkommer ved å sette elementer slik at de danner en trekant. Det blir det samme som å legge sammen et visst antall naturlige tall. De fire første trekanttallene blir da $T_1=1, T_2 = 3, T_3 = 6$ og $T_4 = 10$.
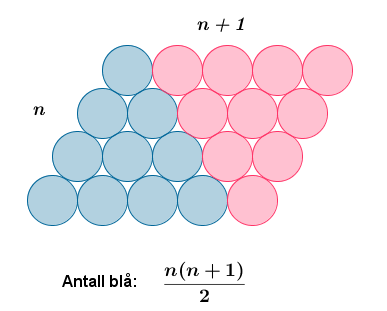
De fremkommer ved å sette elementer slik at de danner en trekant. Det blir det samme som å legge sammen et visst antall naturlige tall. De fire første trekanttallene blir da $T_1=1, T_2 = 3, T_3 = 6$ og $T_4 = 10$. | Visuelt bevis for formelen: | Induksjonsbevis for formelen: |
 |
$$\frac{n(n+1)}{2}-\frac{(n-1)(n)}{2}=n$$ |
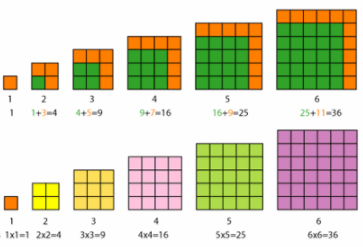

| 1 | 8 | 27 | 64 |
