Form og bevegelse
- Kommutativ lov
- Assosiativ lov
- Kvadratsetningene
- Geometiske bevis av kvadratsetningene
Avbildning i geomtrien dreier seg om hvordan geoemtriske figurer er like hverandre, eller om de er en forandring av en form til en annen.
Kongruens
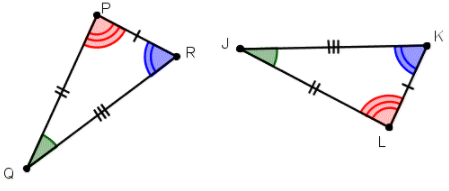To trekanter sies å være kongruente med hverandre hvis alle sider og alle vinkler er like. For å avbilde den ene på den andre trenger vi to typer bevegelser. Det ene er en rotasjon slik at de to trekantene får samme retning. Det andre er en translasjon slik at de to figurene dekker hverandre.
Fysiske figurer kan man si er kongruendte med hverandre fordi hverken lengder eller vinkler forandrer seg når de beveges.
Formlikhet
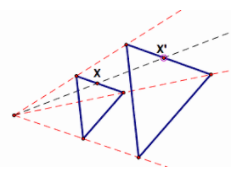To trekanter er formlike hvis alle vinklene er like hverandre i de to trekantene. Man kan avbilde den ene på den andre ved en rotasjon og en homotetisk avbildning. To trekanter er homotetiske til hverandre hvis linjer gjennom samsvarende hjørner møtes i samme punkt, og samsvarende linjer er parallelle.
Perspektivisk
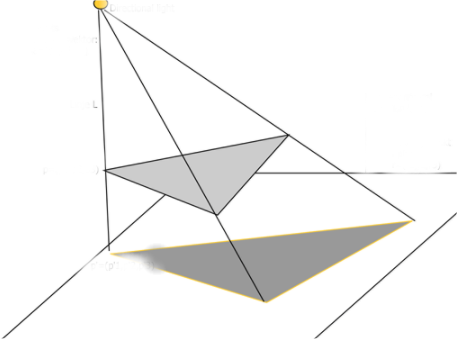To trekanter er perspektiviske til hverandre hvis linjer gjennom samsvarende hjørner møtes i samme punkt. Har vi en punktuell lyskilde vil skyggen av en trekant være en perspektivisk avbildning av denne.