Perspektivtegning
- Perspektivtegning
- Forsvinningspunkt
- Etpunktperspektiv
- Topunktperspektiv
- Trepunktperspektiv
- Parallellperspektiv
- Perspektivisk mønster
Perspektivtegning er gjengivelse av geometriske figurer og gjenstander slik det ser ut fra en viss synsvinkel. Når gjenstander har parallelle sider vil de se ut som om disse parallelle sidene møtes i et og samme punkt. For eksempel vil kantene på en vei nærme seg hverandre når horisonten. Vi kaller det punktet de nærmer seg forsvinningspunktet. Det kan være ett, to, tre eller ingen forsvinningspunkter i en tegning. Vi ser på en et punkts perspektiv, topunktsperspektiv , trepunktsperspektiv og et planmønster i perspektiv.
Ettpunktsperspektiv
 I ettpunktsperspektiv samles linjene i dybden i et punkt, mens linjene i bredden og høyden er parallelle. Typisk blir ofte veier og det indre av rom fremstilt slik.
I ettpunktsperspektiv samles linjene i dybden i et punkt, mens linjene i bredden og høyden er parallelle. Typisk blir ofte veier og det indre av rom fremstilt slik.
En regulær følge i dybden slik som stolper med like langt mellomrom danner en geometrisk følge. Den kan konstrues slik som en geometrisk følge konstrueres.
Topunktsperspektiv
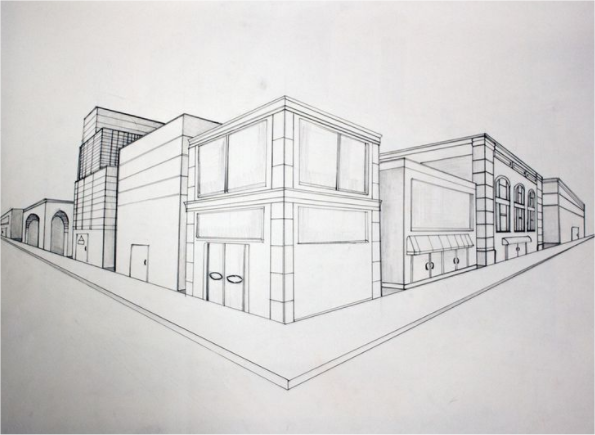 Topunktperspektivet fremkommer når to perspektivpunkter legges på en horisontlinje. Her er det perspektiv fra to siden, mens høydelinjene er parallelle. Typisk fremstilles bygninger og rettvinklete objekter på denne måten.
Topunktperspektivet fremkommer når to perspektivpunkter legges på en horisontlinje. Her er det perspektiv fra to siden, mens høydelinjene er parallelle. Typisk fremstilles bygninger og rettvinklete objekter på denne måten.
Trepunktsperspektiv
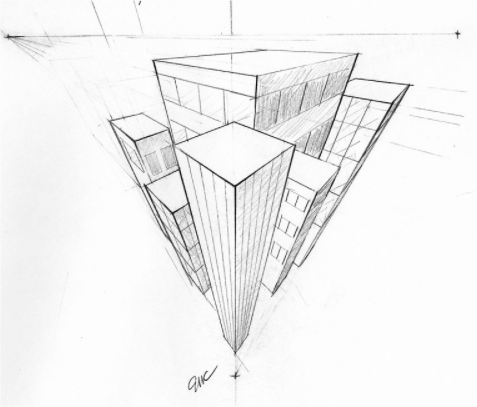 Trepunktperspektivet fremkommer når ingen av linjene er parallelle, men der de tre retningene i rommet møtes i tre punkter.
Trepunktperspektivet fremkommer når ingen av linjene er parallelle, men der de tre retningene i rommet møtes i tre punkter.
Vis →
Dette perspektivet brukes for eksempel når man har med høye bygninger å gjøre, enten sett ovenfra eller nedenfra.
Parallellpersepktiv
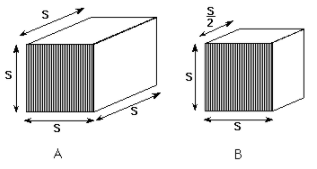 Man kunne egentlig også snakke om nullpunktperspektiv. Da har vi ingen forvinningspunkter, men linjene i de tre romdimensjonene er paralelle. Dette perspektivet kaller man for parallellpserspektiv.
Man kunne egentlig også snakke om nullpunktperspektiv. Da har vi ingen forvinningspunkter, men linjene i de tre romdimensjonene er paralelle. Dette perspektivet kaller man for parallellpserspektiv.
Hvis vi har parallelle linjer lodrett og vanrett, så vil den tredje retningen danne en vinkel på ca. 30 grader i forhold til horisontalplanet. Hvis man skal tegne en kube i dette perspektivet vil det se naturlig ut når man har lengden i den tredje retningen halvparten av retningene vertikalt og horisontalt.
Regulære mønster
Regulære mønster kan også fremstilles ut fra topunktperspektiv. Vi må da legge inn et tredje perspektivpunkt på horisontlinjen. Da fremkommer regulære firkant og sekskantmønster i perspektiv, det såkalte Møbiusnettet.
Avstandene i et regulært topunktperspektivmønster danner en vekstfølge.

 I ettpunktsperspektiv samles linjene i dybden i et punkt, mens linjene i bredden og høyden er parallelle. Typisk blir ofte veier og det indre av rom fremstilt slik.
I ettpunktsperspektiv samles linjene i dybden i et punkt, mens linjene i bredden og høyden er parallelle. Typisk blir ofte veier og det indre av rom fremstilt slik. Topunktperspektivet fremkommer når to perspektivpunkter legges på en horisontlinje. Her er det perspektiv fra to siden, mens høydelinjene er parallelle. Typisk fremstilles bygninger og rettvinklete objekter på denne måten.
Topunktperspektivet fremkommer når to perspektivpunkter legges på en horisontlinje. Her er det perspektiv fra to siden, mens høydelinjene er parallelle. Typisk fremstilles bygninger og rettvinklete objekter på denne måten. Trepunktperspektivet fremkommer når ingen av linjene er parallelle, men der de tre retningene i rommet møtes i tre punkter.
Trepunktperspektivet fremkommer når ingen av linjene er parallelle, men der de tre retningene i rommet møtes i tre punkter. Man kunne egentlig også snakke om nullpunktperspektiv. Da har vi ingen forvinningspunkter, men linjene i de tre romdimensjonene er paralelle. Dette perspektivet kaller man for parallellpserspektiv.
Man kunne egentlig også snakke om nullpunktperspektiv. Da har vi ingen forvinningspunkter, men linjene i de tre romdimensjonene er paralelle. Dette perspektivet kaller man for parallellpserspektiv.