Enhet mellom geometri og algebra

- anskuende forståelse av rommet

---

I den greske tid var det harmoni mellom legeme og sjel, man talte om en "sunn sjel i et sundt legeme". Vi finner denne enhet også i den greske geometri, her var de geometriske elementer og de geometrisk størrelser ett. I den nyere tid spaltet denne enhet seg opp. Aritmetikk og algebra ble anvendt på den ytre verden, man ville beregne det som skjedde her. På den annen side utviklet den rene geometrien seg ved at man undersøkte perspektivet. I vår tid ser vi at geometri og aritmetikk igjen finner sammen. I oppdagelsen av den geometriske algebra får de geometriske objekter så å si en indre side. For å se denne enhet kan man til å begynne med få tak i den enhetlige struktur som vever i fenomenene. Denne strukturen finner man også i tilknytning til Goethes fargelære.

Historisk innledning

I den nyere tid vendte mennesket sitt blikk utad for å begripe, for å få næring til den begynnende bevissthetssjel som utviklet seg i det indre. Man begynte å beregne forholdene i den ytre verden, - naturvitenskapen oppstod. Galileo Galilei fant bevegelseslovene, og Kopernikus og Kepler beregnet hvordan himmellegemene beveger seg. Lord Bacon uttalte: Mål og vei alt, og gjør det som ikke er målbart - målbart.

Denne holdning var et brudd med den greske matematikk. Her var det en enhet mellom geometri og aritmetikk og algebra. De geometriske elementene var ikke bare figurer, men også størrelser. En linje var det vi i dag kaller et linjestykke, det vil si et geometrisk objekt med en lengde, mens et rektangel var en flate med viss form og størrelse. Produktet av to linjer ble et rektangel, - både rektangelets form og størrelse oppstod gjennom produktet.

I den nyere tid skilte dermed geometrien og aritmetikken lag. Aritmetikken ble brukt på ytre punktuelle gjenstander der disse i seg selv var døde objekter, og beregningen gikk ut på å finne relasjoner til andre objekter. Selve objektene hadde ikke lenger en aritmetisk side. Ved Newtons gravitasjons-lov blir også vekt en relasjon mellom to materielle legemer, og ikke noe som egentlig tilhører objektet. Rene Descartes utviklet et system for å kunne beregne punktuelle objekter, og punktet ble det sentrale objektet i geometrien.

På den annen side utviklet geometrien seg fra anskuelsen av den ytre verden. I maleriet ville man har frem verden slik den fortonet seg fra malerens ståsted og perspektivlæren oppstod. Denne ble utviklet videre til de første kimene til den projektive geometri av Girard Desargues og Blaise Pascal.

Nå var det en annen utvikling som fant sted som er av avgjørende betydning for utviklingen av matematikken. Her var det ikke noe ytre man ville ha tak på, men det var en ren virksomhet i det indre. I den greske og arabiske tid kunne man løse ligninger opp til andre grad. Under merkelige omstendigheter gikk man nå løs på ligninger av tredje og fjerde grad. Disse kunne man etter hvert løse, men det innebar at man måtte se nærmere på tall som kvadratroten av minus en. Læren om de komplekse tall ble utviklet.

$$I=\sqrt{-1}$$ $$I^2=-1$$

Disse tre momentene, - den rene geometri, koordiantsystemene og de komplekse tall, - er tre kimer til det som er matematikken i dag, og som også har ført til at geometri og aritmetikk igjen nærmer seg å kunne bli betraktet som en enhet.

De nye tallsystemer, hyperkomplekse tall

Hermann Wessel førte sammen de komplekse tall og geometri. Dette blir en geometri i planet. Rowan Hamilton søkte å utvikle noe lignende for rommet, altså et system med tre tall. Han fant frem stil et system med fire komponeter, - en skalar og tre komplekse komponenter, - de såkalte kvaternioner: \[(\; 1 \;,\; u \;,\; v \;,\; w \;)\]Her er det slik at hver av de tre komplekse komponentene gir et kvarat som er lik -1. I tillegg er produktet av to komponenter lik den tredje komponentene.

$$u^2=v^2=w^2 =u\cdot v \cdot w -1 $$

Hamilton anvendte disse tallene på det tredimensjonale rom, og regning med kvaternioner ble en sentral virksomhet utover på 1800 tallet.

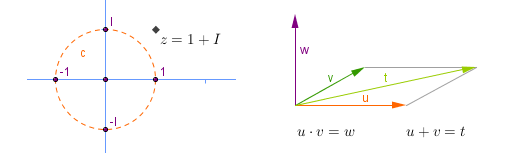
Komplekse tall og kvaternioner

Clifford algebra

William Kindon Clifford fant at kvaternionene kan sees på i sammenheng med fire andre komponeter, slik at det i alt blir åtte komponeter i disse hyperkomplekse tallene. Til forskjell fra kvaternionene er kvaratene av tre av komponentene lik 1, mens kvadratet av den fjerde komponenten er lik 1. Kaller vi komponetene i , j , k og I har vi følgende forhold

$$i^2=j^2=k^2=1 \;\;,\;\; I^2 = -1$$ $$ i \cdot j = w \;\;,\;\; j \cdot k = u \;\;,\;\; k \cdot i = v$$

David Hestenes har utviklet anvendelsen av dette systemet på de mest ulike områder. I samarbeide med Ranatus Ziegler utviklet han dette systemet for den projektive geometri. Charles Gunn, som har samarbediet med Oliver Conradt, anvender systemet på det såklate Cayley-Klein rommet i sin doktorgrad og har utarbeidet flere skrifter om geometrisk algebra (clifford algebra)

Ordenen mellom elementene

Når de eksta komponetene kommer til får vi en orden som ligner på den orden fargene har i Goethes fargesirkel.

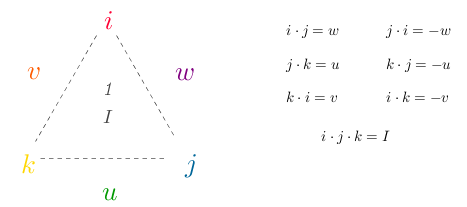
Denne orden har jeg gått inn på ved en tidligere anledning. Vi ser den samme orden i en elemetær likesidet trekant. Her har vi tre punkter, og vi har tre linjer som forbinder disse. Dette svarer på sett og vis til de to triplettene vi har sett på. For at det geometriske og algebraiske skal falle helt sammen må vi utvide den geometriske strukturen til en dobbelttetraedriske struktur. Dett har Ingo Nussbaumer gjort med fargene. Han har latt sort og hvitt inngå i systemet og sammen med de seks fargene i frgekresten danner fargene et dobbelttetraeder, eller en kubisk struktur.

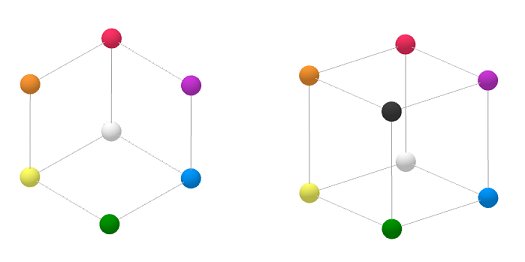
Fra fargesirkel til fargekube

Den kubiske, eller dobbeltteraedriske orden ser vi også er strukturert. Vi har to grupper med tre elementer i hver. For eksempel er fargene fordelt i de tre primærfargene magenta, blå og gul, og i de tre komplementære grønn, orange og fiolett. I tillegg har vi de to polene hvitt og sort. Vi kan dermed sett opp tallfølgen 1, 3, 3 og 1. Dette er en rad i pascals trekant som kommer til anvendelse ved kombinatorikk, og egentlig er det slik at denne orden kan sees på som en kombinatorisk orden.

1 - 3 - 3 - 1 strukturen er en rad i pascals trekant

Ordenen gjør seg også gjeldene som struktur i geometriske fenomener. Vi kan se dette i den grunnleggende struktur mellom plan linjer og punter i rommet. Har vi gitt tre plan i rommet danner to og to av disse mellom seg, slik at det blir tre linjer, og alle plan og linjer danner går gjennm et punkt. Vi har dermed strukturen 1 rom, tre plan, tre linjer og et punkt. Vi ser også at vi går nedover i dimensjonene her, fra rommet med 3 domensjoner, til plan med 2, linjer med 1, og punktet som er 0 dimensjonalt.

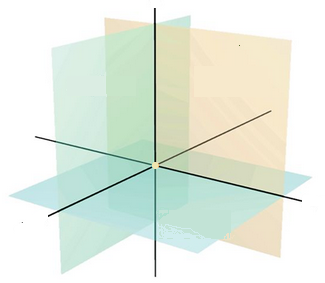
1 - 3 - 3 - 1 strukturen.

Discobolus