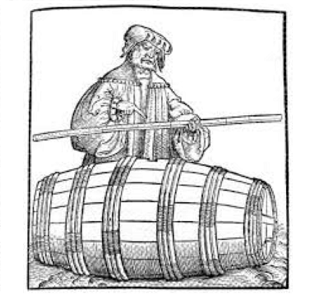
Målestav
Volumet blir lest av ved å finn halve tverrmålet.
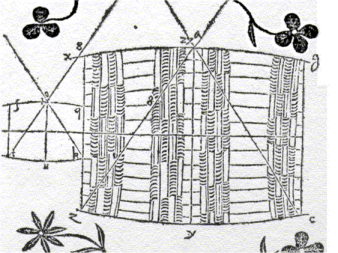
Illustrasjon fra:
"Nova stereometria doliorum vinariorum"
(Ny stereometri av vintønner)
Tønnen har ellipstisk form
Her er vi ved en prinsipielt viktig punkt. Når Kepler sier at tønnen er ellipstisk, så kan jo det være tilnærmelsesvis. Men forsåvidt som tønnen har ellipstisk form vil det som utregnes stemme. Dette er det vitenskapelige moment, ikke hvorvidt ideen faller eksakt sammen med sansingen.
Kjeglesnittene mellom den rette og krumme linje
Kepler plasserte kjeglesnittene mellom den rette og krumme linje. Hyperbelen er i denne henseende mest lik linjen, mens ellipsen er mest lik sirkelen. Lar vi ellipsen vokse til uendelig, får vi parabelen. Og lar vi den nederste delen av til hyperbelen gå til uendelig får vi igjen parabelen. Parabelen er dermed den utlignende kurven mellom den krumme og rette linje.
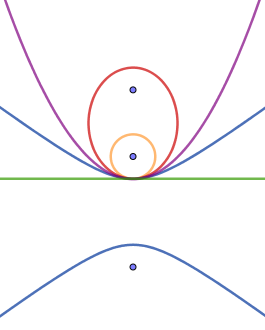
Kjeglesnittene mellom den rette og krumme linje
Kepler plasserte kjeglesnittene mellom den rette og krumme linje.
Hyperbelen er i denne henseende
mest lik linjen, mens ellipsen er mest
lik sirkelen. Lar vi ellipsen vokse til uendelig,
får vi parabelen. Og lar vi den nederste delen av
til hyperbelen gå til uendelig
får vi
igjen parabelen. Parabelen er dermed
den utlignende kurven mellom
den krumme og rette linje.


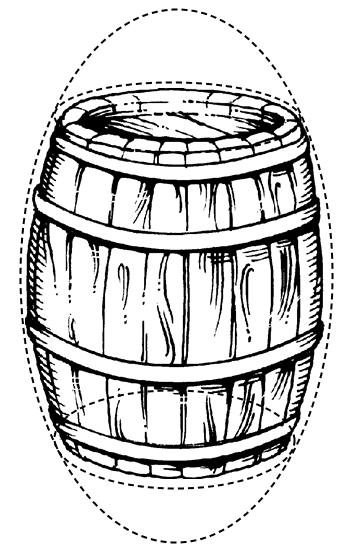
Tønnen har en elliptisk form.
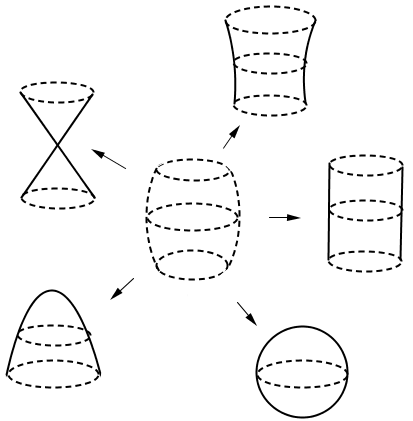
Tønnen kan anta mange former, og for hver form oppstår er spesielt utrykk for tønneformelen.
Keplers tønneregel
- og vitenskapelige aspekter ved denne
Morten Eide
Keplers finasierte selv utgivelsen av boken om "Volummål for tønner" fordi ingen på hans tid så verdien av dette verket. Den viser seg å inneholde kimer til flere av områdene som skulle blir sentrale i viteskpaen senere. Det vesentlige filosofisk meoment dreier seg om individets frigjøring fra det vedtatte, til å sette inn et personlig syn.
Johannes Kepler (1471-1530) er mest kjent for sitt astronomiske verk. Men han var virksom på en rekke områder, og han la for eksempel grunnlaget for den moderne optikk. I sitt
I det gangske ukjete arbeidet "Nova stereometria doliorum vinariorum"(Ny stereometri av vintønner) tar han fatt på et volumroblem, og i behandlinen av problemet kommer han ganske nær opptil den moderne infinitesimalteori. Leibniz, en av de senere grunnleggerne av infinitsimallæren kjente godt til Keplers arbeid.
Den viser også et teorem som er vandlingsbart, det vil si at formen av det gjør det mulig å regne ut flere typer volum med samme formel. Rudolf Steiner sier i innledningen til sin bok "Goethes naturvitenskaplige skrifter" at "Goethe er biologiens Kepler og Kopernikus". Han tenkte da på Goethes morfologiske ide som kommer blandt annet til utrykk i "Plantenes metamorfose". Men man kan si at Kepler selv langt i retnig av en å forstå begreper morfologisk, det vil si at man har for seg et fast begrep som kan anta mange former. Dette kommer til utrykk i hans behandling av kjeglesnittet der parabelen for eksempel anskues som en uendelig lang ellipse
Et erkjennelsesteoretisk moment er at vi her har et eksempel på hvordan mennesket stiller seg kritisk til det vedtatte , og tenker tingene på nytt fra begynnelsen av. Kepler forteller i boken hvordan han begynte arbeidet med å beregne volumet av vintønnen.
Forundringen
Også dette arbeidet har sitt utspring i at Keplers undrer seg over noe han blir oppmerksom på. Han skriver:
Da jeg mot slutten av November innførte en ny hustru i mitt hus, var det nettopp på den tiden at mange lektere med rik og utmerket vin førtes opp Donau. Det var da min plikt som ektemann og god far å forsørge mitt hus med nødvendig drikke. Jeg lot derfor skaffe ganske mange tønner vin som jeg selv innførte i huset.
Fire dager etter kom selgeren med en målestang som han benyttet som eneste verktøy til å måle volumet, uten å ta hensyn til tønnes form, og uten å gjøre noen beregninger. Han stakk nemlig spissen av jernstangen på skrå gjennom påfyllingshullet til den fulle tønnen, til den traff i kanten mellom lokket og tønnesiden. Han leste da av på stangen hvor mye vin som var i tønnen.
Det syntes meg forunderlig at det var mulig å finne volumet til tønne ved å måle halve tverrmålet, og jeg tvilte på påliteligheten til denne måling.
Ellipsoide
Kepler griper fatt i probemstillingen. Det første han gjør er å begripe tønneformen som en avkappet ellipsoide. Her er vi ved et erkjennelsesteoretisk viktig moment. Når man sammenligner tønner med ellipseformen så ser man at det stemmer. Men helt eksakt kan det ikke bli, - det kan være en litt annen form, og det er også unøyaktighet i utskjæringene av treet. Dette er liekvel ikke det veentlige. Forsåvidt som tønnen er en elippsoid kan man bestemme volumet. Han har jo tidligere begrepet planetbanene som ellipser og kan bruke resultater herfra til det nye arbeidet.
I dag ville vi bruke integralregning for å finne volumet. Det kan settes opp slik:
$$y^2=a x^2+b x +c$$ Vi integerer: $$V=\int_p^q ax^2+ b x+ c \;\;dx$$ $$ V=(q-p) (6 c + 3 b p + 2 a p^2 + 3 b q + 2 a p q + 2 a q^2)/6$$ Her er jo $(q-p)$ høyden i tønnen. Utrykket i parantesen er gitt som $ y(p)^2+4 y((p+q)/2)^2 + y(q)^2$ og dermed har vi formelen.
Den bevegelige ide
Den formelen vi nå har kommet frem til, $$V=\frac{(G+4 M+T)h}{6}$$ kan anvendes til å finne mange typer volum. Det viser seg også at formelen spesialiserer seg til ulike volumutrykk som vi kjenner fra før. Ved å anta bestemte verdier for henholdsvis grunnflate (G), midtareal (M) og toppflate (T) oppstår de andre volumutrykkene.
SylinderNår vi har en sylinder for eksempel, vil alle arelaene bli like.
Vi har da:$$V=\frac{(G+4\cdot G+G)h}{6}=\frac{6 \cdot G \cdot h}{6} = G\cdot h$$ som er det kjente volumet for en sylinder.Kule
Kulen kan også betraktes som en tønne der både grunnflaten og topplaten er null. Det fører til:$$V=\frac{(0+4\cdot G+0)h}{6} = \frac{2 G \cdot h}{3}$$ Når vi setter inn $h= 2r$ og $F= \pi r^2$ oppnår vi $$V=\frac{4\pi r^3 \cdot 2 r}{6}=\frac{4\pi r^3}{3}$$ som er det kjente utrykk for volumet til en kule.Kjegle
Volumet til en kjegle kan vi finne ved å se på volumet til en dobbeltkjegle. Her er det midtflaten som blir null og utrykket tar da formen: $$V=\frac{(G+0+G)h}{6} = \frac{2 \cdot G \cdot h}{6}= \frac{G \cdot h}{3}$$ Her er jo høyden til dobbeltkjeglen det dobbelte av en enkeltkjegle, slik at en volumet av en enkel kjegle får samme uttrykk.Parabol
I en parabol med gitt grunnflate G, er den miderste flaten G/2, og den øverste lik 0. Her blir altså volumet: $$V=\frac{(G+4 \cdot G/2+0)h}{6} = \frac{G \cdot h}{2}$$ Utledning parabol midtsnitt ▼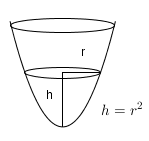 Den enkleste parabelen har ligningen $y=x^2$. For en parabol blir dette $h = r^2$. Da kan vi skrive arealtet av et snitt $F = \pi \cdot r^2 = \pi \cdot h$. For midtsnittet er høyden er lik $\frac{h}{2}$ arealet av midtsnittet blir derfor $\frac{\pi \cdot h}{2}$. Det vil si at midtsnittet er halvparten av grunnflaten.
Den enkleste parabelen har ligningen $y=x^2$. For en parabol blir dette $h = r^2$. Da kan vi skrive arealtet av et snitt $F = \pi \cdot r^2 = \pi \cdot h$. For midtsnittet er høyden er lik $\frac{h}{2}$ arealet av midtsnittet blir derfor $\frac{\pi \cdot h}{2}$. Det vil si at midtsnittet er halvparten av grunnflaten.
Elliptiske kurver

Tønneformelen gjelder også for tredjegradskurver, og enkelte vaser har slik form.
Kjeglesnittene er spesialvarianter av dissse kurvene. Andre utrykk kan være vaseform. En spesiell form finner vi i luftballonger. Det gjør at vi enkelt kan finne volumet av slike ballonger også.
Naturvitenskap og matematikk
Vi er ved disse betraktningene ved grensen mellom matemmatikk og naturvitenskap. Den alminnelige vitenskaplige holdning har vi idag fra Carl Popper og Thomas Kuhn. Vi kan ikke vite sikkert. Det er på et vis riktig, men er også feilkatig med hensyn på egentlig vitenskap. Det som i denne sammenheng kan falsifiseres er hvorvidt en tønne har en ellipseform. Men det kan ikke falsifiseres en gang for alle, det må bekreftes eller avkreftes i hvert tilfelle. Eventuelt at man sier at tønnen har nesten ellipseform. Når man så har avgjort i hvilken grad tønnen eller en annen form har den riktige form, så kan fromelen anvendes.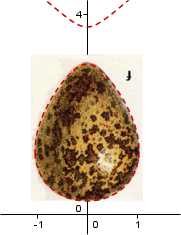
Også egget har en elliptisk tredjegradsform.
Avsnitt 2
Tekst i avsnitt 2
Avsnitt 3
Tekst i avsnitt 3