I de åndsvitenskaplige fremleggelser stiller Rudolf Steier ofte frem hvordan motsridende krefter virker i verdensutviklingen. Vanligvis ser man utelukkende på innholdet i det som legges frem, men Rudolf Steiner gjør ofte oppmerksom på at det ligger en streng metodikk til grunn. Når man ser på den vitenskapelige struktur her, finner man ikke den vanlige vitnskaps idealer, men man finner Goethes naturviteskaplige metode. Denne har evnen til å trenge frem til det menneskelige. Men det viser seg at også den alminnelige vitenskap har disse strukturen i seg, man må bare søke dem. Når man vinner inniskt i disse, da viser det seg en eksakthet i de metoder Goeteh og Steiner anvender, som man kan ta med seg videre.

Strukturen i Goethes fargelære er en helt annen enn den man vanligvis finner i vitenskapen. Likevel er det denne strukturen som henger mest sammen med de dypere mysterier i naturen. I denne tas utgangspunkt i at naturen opptrer polart, og er slik sett nært det menneskelige.

Foruten å være mønstergyldig når det gjelder metode oppviser Goethes fargelære strukturer som synes å peke dypt inn i verdenshendelsene. Selv om man ikke skal trekke sammenligninger for langt, og særlig ikke tenke seg at det ene er et bilde av et annet, kan man fordype områder ved å se på de felles strukturer som oppstår.

Den kosmiske utvikling

I 'Mysteriestätten des Mittelalters' går Rudolf Steiner inn på verdensutviklingen og her kommer begrepene fra fargelæren tydelig frem. Han beskriver hvordan Saturntilstanden dannes av første hierarki, og ved samvirke mellom Keruber, Troner og Serafer oppstår en varmetilstand. Soltilstanden fremkommer ved at det annet hierarki kommer til, og det dannes lys der luften oppstår som en slags skygge av lyset. En polaritet er oppstått. På det neste trinn kommer det tredje hierarki til, og den kjemiske eller fargeeteren dannes ved at dette hierarki bringer lyset inn i skyggen, og skyggen inn i luften. Fargene oppstår, og alt som er beslektet med fargene. Vannet dannes her som skyggen av den kjemiske eteren. Det fjerde trinn er jorden og her oppstår vesener med indre liv og ytre konturer.

Vi ser her mye av strukturen i Goethe fargelære i utvidet forstand. Et sted(hvor?) sier Rudolf Steiner at noe av poenget med å sette seg inn i verdensutviklingen er å danne organ for å skue tilblivelsesprosessene i verden i det hele tatt.

Nå kan det være slik at denne strukturen kan ansees å være dannet ut fra et kunstnerisk sinnelag, og at den ikke har så mye å gjøre med de strenge vitenskapene slik de har utviklet seg i vår tid. Vi skal i det følgende se på hvordan strukturen også gjenfinnes i matematikk og fysikk. Men først ser vi gi en skisse av det som viser seg i selve fargelæren.

Goethes fargelære

Goethe går ut fra polariteten mellom lys og mørke i sin fargelære, og ut fra et samspill mellom lys og mørke oppstår fargene. På den ene siden oppstår de varme fargene gult og rødt ved at lyset gjennomtrenger mørket, og på den andre siden oppstår de kalde fargene blått og fiolett ved at mørket viser seg gjennom lyset.

Det er dette Goethe kaller urfenomenet, at fargene oppstår i et dynamisk samspill mellom lys og mørke. Men dette er ikke alt, det er også andre fenomener som er til stede.

Grønnfargen oppstår så ved at det gule fra den ene siden blander seg med det blå fra den andre siden, og purpur oppstår ved at det røde fra den ene siden møter det fiolette fra den andre siden.

Dette må vi også kalle fenomener av et slag. Vi kan ikke dedusere at det må dannes grønt for eksempel. Dette er de momenter man henter ut fra iakttagelsene. Det er da et spørsmål hva disse fenomenene kalles, - er de en del av urfenomenet, eller blir det annerledes? I hvert fall hører de til fenomenområdet.

Fargesirkelen

Det neste som foreligger er at de fargene som oppstår danner et abstrakt system. De seks fargene som er kan stilles sammen i ent krets, den såkalte Goethes fargesirkel.

Man stiller her opp de varme fargene på den ene siden og de kalde på den andre, og mellom disse setter man grønt der blått og gult møtes, og purpur der rødt og fiolett møtes. Det bemerkelsesverdige man kan se vider er at fargene i kretsen er polare til hverandre på flere måter. Ser man på den ene fargen lenge, vil vi få et etterbilde av den motsatte fargen. Polariteten viser seg også ved prismatiske forsøk, polare fager som overlapper frembringer grått. I dette blir det også klart at lys og mørke begge har del i frembringelsen av fargene.

I tillegg til å tale om fargenes tilsynekomst og deres relasjoner til hverandre går Goethe også inn på hvordan fargene virker på oss. Rødt virker for eksempel dramatisk, mens blått virker rolig.

Vi har dermed å gjøre med tre nivåer innen fargelæren.

• Hvordan fargene oppstår i det fysiske mellom lys og mørke
• Hvordan relasjonene mellom fargene er og den orden de danner
• item Hvordan fargene virker sjelelig.

Vi skal se at disse nivåene også på sett og vis viser seg i geometrien.

Geometri

Spirene til den projektive geometri finner vi på 1600 tallet ved Desargues og Pascals arbeider. Virkelig vind i seilene fikk den på begynnelsen av 1800 tallet. Da oppdaget Poncelet den projektive metode, og det såkalte dualitetsprinsippet ble oppdaget. Her finner man også innen geometrien et polaritetsforhold.

Vanligvis kan man tenke slik at punktet er det mest sentrale, og at andre elementer bygges opp av disse. Ved nærmere studier ser man at det er en likeverdighet mellom punkt og linjer i den projektive geometrien. Akkurat slik Goethe hevdet at mørket spiller an aktiv rolle, slik oppdaget man at linjen hadde samme værenskarakter som punktet. Det gir seg utrykk elementært i det at to punkter har en felles linje, men at man kan vende om på dette og si at to linjer har et felles punkt. Faktisk er det slik at alt man kan si om punkters forhold til linjer, kan man si om linjers forhold til punkter.

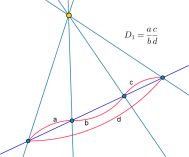
Dobbeltforholdet

Og slik som lys og mørke virker sammen og gir fargen, slik kan vi se at punkt og linje virker sammen og gir tallforhold.

Oppstaåen av dobbeltforholdet

Et aspekt ved at man danner polaritet mellom punkt og linje er at man ikke bare sier at linjer består av punkter, men også at punkter består av linjer. Punktet stråler liksom ut linjer.

Når et punkt slik stråler ut linjer kan disse treffe en linje på tvers, og bryter gjennom denne. Mellom disse oppstår det skjæringspunkter, og mellom punktene her oppstår det linjestykker.

Hvis vi fra et trekker vi fire linjer som skjærer over en annen linje, da oppstår det fire punkter ($A$,$B$,$C$,$D$) på denne linjen. Mellom linjene danne det linjestykker. Nå setter vi inn lengder på linjestykkene. Disse lengdene står i et visst forhold til hverandre, som vi kaller dobbeltforholdet. \[D=\frac{AB}{BC}\frac{CD}{DA}\]

Dette dobbeltforholdet viser seg å være fundamentalt i den projektive geometri. Det viser seg for det første at når de fire linjene er gitt kan vi bevege den gjennomstrålte linjen, og dobbeltforholdet vil alltid være konstant.

Vi har altså: Gitt et punkt som stråler ut fire punkter som møter en linje. Da oppstår et dobbletforhold mellom de fire punktene.

Slik som fargene på sett og vis er subjektiv - objektive, slik er også dobbelforholdene subjekiv - objektive. Hvis vi sier at selve geometrien er objektiv, så er det vi som føyer til størrelsene der linjestykker oppstår.

Seks dobbelforhold

Sammenhengen med fargelæren får en videre bekreftelse ved at det i alt kan dannes seks dobbeltforhold mellom de fire punktene.

Vi kan går seks veier fra punkt $A$, gjennom de andre punktene og tilbake til $A$. De seks dobbeltforholdene som oppstår slik kan man sette opp i en krets, og relasjonen mellom forholdene blir et lignende som det vi har mellom fargene i fargesirkelen. To polare dobbeltforhold danner produktet 1, og produktet av to dobbeltforhold som ligger 120 grader fra hverandre gir dobbeltforholdet mellom dem.

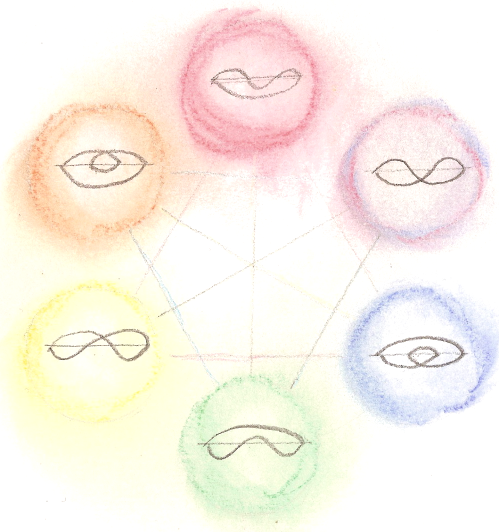
Et forhold til hersker mellom dobbeltforholdene. Slik produktet av to og to blir 1, slik blir også summen av to og to av dem 1.

Bevegelsesmomenter

Det siste forhold gjør at når vi kjenner et dobbeltforhold kan vi finne de seks andre i kretsen. Siden produktet av to motstående dobbelt forhold er 1, kan vi finne det motsatte når vi kjenner det ene ved funksjonen $$y = \frac{1}{x}$$. Og ser vi på forholdet der summen av to dobbeltforhold er 1, kan vi finne det andre ved funksjonen $y=1-x$. I alt dannes det seks slike funksjoner, som også kan setter opp i samme type krets som dobbeltforholdene. Og nå er det slik at hver funksjon utrykker en kvalitet. Funksjonen $y = \frac{1}{x}$ vender så og si opp ned på et annet tall, funksjonen $y=1-x$ hva som er igjen av helheten og funksjone $y = x$ tredje lar alt være i ro. Man kan meditere på om slik overganger frembringer visse fornemmelser.

1. Dobbeltforholdenes fremkomst.
2. Algebraiske relasjoner.
3. Gruppeegenskaper.

Vi skal nå se om vi finner denne strukturen også i mekanikken.

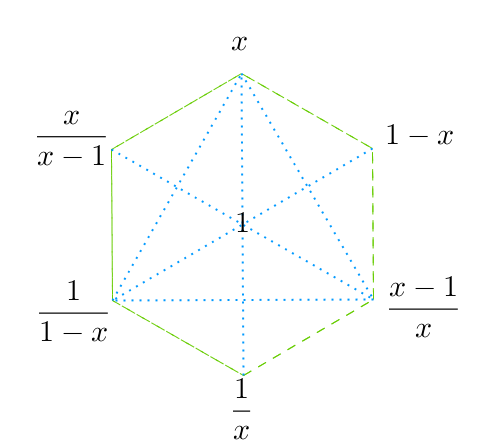
Gruppe-krets

Mekanikk

En foredragsserie av Rudolf Steiner har tittelen 'Bevissthet, form og liv'. Dette oppsettet gir opphav til å betrakte bevissthet og form som polariteter. Vi kunne også si at bevissthet, eller bevissthetens lys er ren bevegelse, mens formene er ren ro.

Når vi skuer ut i verden står vi ovenfor en formverden. Når vi så virker i verden oppstår liv. Og nå oppstår en differensiering som bringer frem begreper vi kjenner fra vitenskapen ellers, også i mekanikken.

Når vi virker i verden virker en kraft. Denne kraft frembringer en bevegelse og endring hos objektet. Vi kaller i livet, og i fysikken, det som foregår for et arbeid på verden.

Går vi enda snevrere inn på hva endringen består i så kan det være at vi løfter en gjenstand en viss høyde. Vi bruker da en viss kraft, og i fysikken har vi et eksakt utrykk for forholdet mellom kraften, høyden vi løfter og arbeidet som blir gjort: \[Arbeid = Kreft \cdot vei\] \[W \; = \; F \cdot s\] Kraft og vei blir her en polaritet. Kraften oppleves hos subjektet, endringen observerer vi i objektet.

I mekanikken er det flere begreper. Når kraften virker en viss tid, kaller vi det en impuls, og impulsen setter i gang en bevegelse, eller endrer en bevegelse. Når man slår en golfball har vi med denne polariteten å gjøre. Også dette er et arbeid, og det kan utrykkes slik:

\[Arbeid = Impuls \cdot fart\]Det er riktigere å si at en impuls endrer en bevegelse. Vi kommer dermed inn på differensialer: \[d W = v \; dI\]som betyr at et lite arbeid blir gjort når vi gir noe en liten impuls.

Den tredje polariteten dreier seg om hvor effektivt arbeidet er. Er vi effektive blir mye arbeid gjort i lopet av en bestemt tid. Effekt og tid blir dermed polariteter. \[Arbeid = Effekt \cdot tid\] Disse tre polaritetene kan settes sammen i en mekanikk-krets. Her blir det ikke helt slik som for dobbeltforholdene, men mer som for fargene. De tre grunnstørrelsene blir kraft, bevegelse og tid, og mellom disse oppstår effekt, impuls og endring. \begin{figure} \centering

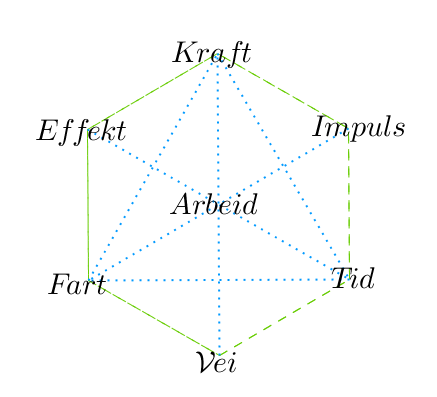
Mekanikksirkel

Kvaliteten på de ulike entiteter}

Slik som Goethe går inn på kvaliteten av fargene kan vi også gå inn på kvaliteten av de ulike fysiske entiteter. Det kan vi gjøre ved å forestille oss en for eksempel en skitur, når man gjør det med en viss ironi.

Vi tenker oss en skiløper som går sin tur opp på en fjell. I den første del av turen går det slakt oppover, men etterhvert blir det brattere. Skiløperens egen kraft som strever oppover må overvinne tyngdekraften i større og større grad. Når han så er kommet til toppen kan han hvile en stund før han setter utfor igjen. Nå er det skiløperen som lar tyngdekraften virke på ham, han må bare være årvåken. Mørket viser seg gjennom lyset.

Her kan vi se de ulike fysiske entiteter. Først har vi den lyse lette bevegelse idet vi sparker lett fra. (gult). Når det blir brattere må vi anstrenge oss, vi opplever kraften i bevegelsen som vi utrykker som effekt (orange rødt). Opplevelsen av at vi overvinner tyngden. På toppen har vi en slags kongefølelse i ren kraft (purpur), vi er i likevekt mellom våre egne krefter og verdens krefter. Når vi setter utfør er det tyngden som virker. Tyngden gir oss impulsen til farten nedover, og det kan være farefullt (fiolett). Hva vi opplever når vi kommer ned på sletten, og t

1. Oppståen av krefter og bevegelser.
2. Algebraiske relasjoner mellom disse.
3. Opplevelse av krefter og bevegelser.

Elektrisitet og andre områder

Den samme struktur gjenfinner vi på andre områder. Innen elektrisiteten finner vi også at statisk elektrisitet oppstår i møtet mellom bevegelse og ro. Det skjer en differensiering og en spenning oppstår mellom ladninger. Slik produktet av kraft og vei var arbeid, slik er produktet av spenning og ladning en potensiell elektrisk energi. Når vi får utladning går det en strøm, og effekten er produktet av strømmen og den spenning som driver den. Slik får vi også ren rekke begreper som igjen går sammen i samme struktur som fargene.

Lignende meditasjoner kan man gjøre innen varmelæren.

Vi ser ved disse eksemplene at strukturene i Goethes fargelære ikke er vilkårlige, men utrykk for en eksakt åndelig orden. Det man kaller naturlover viser seg som uttrykk for levende ideer. I letingen etter hva man fornemmer ved de ulike farger, krefter og bevegelser nærmer man seg også ånden i naturen.

Den levede natur

Når man har tilegnet seg en forståelse av eksaktheten i polaritetstanken, da får man også lettere tilgang til å se etter denne der man i første omgang ikke har en eksakt innsikt. Man bærer på sett og vis eksaktheten i seg, og er ikke så bekymret for at alt ikke viser seg med en gang. Man beveger seg så og si fra å ha en mening om tingene til å ha bevissthet om hendelsene. Vi skal ikke gå nærmere inn på dette nå, men bare sette frem et par momenter.

Man kan være med på den tesen at planten blir til mellom solen og jorden, slik for eksempel George Adams ser det. Solen er her lyskraften og jorden er det mottagende formbare. Når disse forenes oppstår liv. Dette liv kommer til utrykk i formens endring, og usynlig i den kraften som er tilstede i vekstprosessen. Ser man bare på formene og formforandringene har vi biologien, ser vi de kreftene som spiller inn har vi det dynamiske prinsipp, og sammen danner de en biologisk dynamisk enhet.

I snevrere forstand ser vi plantene som utvikler seg fra frøet og som når til en slags fullendelse i blomsten. Denne svever mellom det sanselige og det oversanselige, og opptrere i alle slags farger. I krystallene ser vi form og farge fremtre som resultat av motstående krefter. Også selve evolusjonen har man forsøkt å se mellom drivende og motvirkende krefter.

Fra 'The Plant Between Sun and Earth'

Lyd, musikk og språk

Det er blitt spurt etter lydenes tilsynekomst i tilknytning til fargenes tilsynekomst. Det er ikke helt klart hva man skal kalle urfenomen her, men leter man etter polariteten her ser man at noe beveger seg, og noe holder igjen. Man kunne si at lydene oppstår i feltet bevegelse, motstand. Det ser man både når det gjelder blåseinstrumenter og strengeinstrumenter.

Musikken oppstår når tallfoholdene kommer inn i lydene, og språket når visdommen kommer inn?

Den vitenskapelige strid i vår tid.

Man kan også betrakte selve den vitenskapelige situasjon som en kamp mellom lys og mørke. Det synes å være på det rene at Rudolf Steiner i sine foredrag la vekt på å utvikle en levende forståelse for sammenhengene i verden. Han legger frem en mengde fenomener fra den åndelige område. Som regel er det ikke plass til å utlegge de strengere tankemessige sammenhengene. De må man se selv.

Vi stiller oss altså på lysets side, men Rudolf Steiner viser til at man også må ha bevissthet om at for kulturutviklingens del har mørket sin andel. Dette kommer tydelig frem i foredragene ‘Mennesket og menneskets åndelige ledelse’. Her blir det satt frem at de tilbakeblitte ånder fra den egyptiske tid virker dynamisk mot de ideelle ånder. Det blir dermed gitt den rette tyngde til det som skal utvikles i mennesket. Alt må prøves mot hverandre, slik det ligger i den naturvitenskapelig metode.

APPENDIX

Vi fordyper her noe ved dobbeltforhodlet.

Slik Goethe søker forholdet mellom lys og mørke ved ulike fargefremtredelser, slik kan vi lete etter om dobbeltforholdet er skjult til stede ved fremtredelsen av tallforhold.

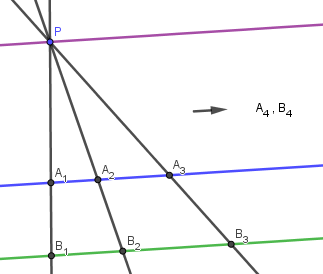
En viktig variant har vi når et av punktene ligger i uendelig. Hvis vi ser på dobbelforholdet\[D_1 = \frac{P_1 P_2}{P_2 P_3}\frac{P_3 P_4}{P_4 P_1} \] og lar $P_4$ gå mot uendelig, da vil \[\frac{P_3 P_4}{P_4 P_1} \]gå mot 1, slik at dobbeltforholdet blir et vanlig forhold \[D_1 = \frac{P_1 P_2}{P_2 P_3} \] En spesialvariant av dobbelforholdet er et vanlig forhold.

Når en av linjene er parallell med linjen som kjærer over, da vil et av skjæringpunkene ligge i uendelig. Vi får at \[ \frac{A_1 A_2}{A_2 A_3}\frac{A_3 A_4}{A_4 A_1} = \frac{B_1 B_2}{B_2 B_3}\frac{B_3 B_4}{B_4 B_1}\]men $\frac{A_3 A_4}{A_4 A_1} = 1$ og $\frac{B_3 B_4}{B_4 B_1}= 1$ slik at \[ \frac{A_1 A_2}{A_2 A_3} = \frac{B_1 B_2}{B_2 B_3}\]