C
Sangaku julekalender
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 |
Klikk i kalenderen for å åpne oppgave.
Sangakuoppgavene er todelte. For det første skal man finne ut hva sammenhengen er, og beskrive denne. Hva vil det si? ▼
Forut for et matematisk bevis ligger at man har funnet et fenomen eller en sammenheng. Det er ikke lett i alminnelighet selv å finne slike sammenhenger, men ved disse sangaku har vi sammenhenger som bare er uttrykkt som bilde. Vi ser på et bilde:
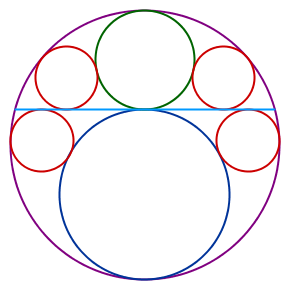
Sammenhengen her kan vi for eksempel beskrive slik: Gitt to sirkler som berører hverandre. Omkring disse ligger det en tredje sirkel med senter på linje med de andres sentre, som berører de to første sirklene. Mellom de to første sirklene er gitt en felles tangent. Vi kan nå legge sirkler mellom tangenten, den ytre sirkelen og en av de indre. Det viser seg at radiene er like store for alle sirklen som kan legges slik.
I klasserommet kan man diskutere seg frem til en beskrivelse.
Sammenhengen her kan vi for eksempel beskrive slik: Gitt to sirkler som berører hverandre. Omkring disse ligger det en tredje sirkel med senter på linje med de andres sentre, som berører de to første sirklene. Mellom de to første sirklene er gitt en felles tangent. Vi kan nå legge sirkler mellom tangenten, den ytre sirkelen og en av de indre. Det viser seg at radiene er like store for alle sirklen som kan legges slik.
I klasserommet kan man diskutere seg frem til en beskrivelse.
Når dette er gjort kan man se om man klarer å bevise det.
Sangaku er en type geometriske oppgaver som ble utviklet i Japan i løpet av Edoperioden. Oppgavene ble malt på tretavler og hengt opp i templene. Noen oppgaver var ganske enkle, mens andre var riktig kompliserte.
Sangaku fra Yamagata
Sangaku fra Yamagata
Send forslag og spørmsål: morten.eide@abelie.no
Se forslag →
(For den enkelte oppgave først etter 7 dager)
Til kalender
C