Sider
| Kongruens og likeformethet | Her finnes de viktigste begrepene knyttet til kongruens og formlikhet. | 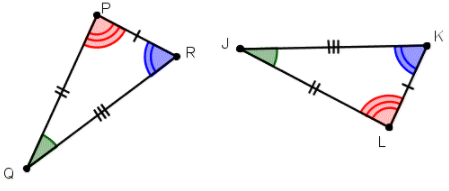
|
|
| Perspektiv- tegning |
Her er en kort fremstilling av perspektivtegning med de ulike perspektiver. Det er også interaktive sider som viser nullpunkt, etpunkts, topunkts og trepunktsperspektiv. | 
|
|
| De klassiske problemene |
En side der de klassiske greske problemene er beskrevet: Vinkelens tredeling, kubens fordobling og sirkelens kvadratur | 
|
|
| Ptolemaios setning |
En side med Ptolemaios setning(er) som dreir seg om forholdet mellom sidene i en firkant innskrevet i en sirkel. Her kan man finne heltallige varianter av strukturen. | 
|
|
| Keplers tønneregel |
En side med Keplers tønneregel. Det er en formel utviklet av Johannes Kepler for å finne volumet av en tønne. Formelen er en generell formel som kan brukes til å finne mange andre volum slik som sylinder, kule, kjegle. | 
|
|
| Vinkel konstruksjon |
En interaktiv side der oppgaven er å konstruere vinkler av ulik størrelse. | 
|
|
| Magisk kvadrat |
En side med magisk $4 \cdot 4$ kvadrat. Ulike kvadrater genereres, og det vises hvordna kvadratene henger sammen med det binære tallsystemet. | 
|
|
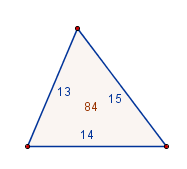
| Herons metode |
Her finnes herons metode for å finne arealet av en trekant når sidene er gitt. En utvidelse er å finne arealet av en innskrevet firkant. Her ser vi på tvillingtalllene. |
Kurs Sandvika
Nytt pr 30.04.2018
Kursoversikten er oppdatert, og det finnes linker til de ulike temaene her: KursoversiktEn oversikt og øvelseside om funksjoner er også lagt ut.
Nytt pr 24.04.2018
Nytt pr 30.04.2018
Det er lagt ut sider med sannsynlighet.Bokstavtelling, myntkast, normalfordeling og fartsmålingNytt pr 24.04.2018
Det er lagt ut en side med funksjonsoppgaver og begreper.Nytt pr 19.03.2018
Det er lagt ut oversikten over kurset med linker. Også en siden med funksjoner kommer etterhvert.Nytt pr 11.03.2018
Det er lagt ut tre sider med kurver. Den ene er om kastebevegelsen. Den andre er om kjedekurven. Den tredje er om eksponentsiell vekst.Nytt pr 21.11
En side med Sage computer er lagt ut her
Nytt pr 20.11
Det er satt inn linker til ulike emner under planen her.
Sidene er figurtall og tallmønster , perspektivtegning og transformasjoner .
Nytt pr 13.11
En side med vekstfølger her.
Nytt pr 10.10
En side med interaktive vinkelkonstruksjoner finnes her.
En side med tallteori med enkle computeroperasjoner finnes her.
Nytt pr 25.09
Endelig mappeoppgave skal også inneholde konstruksjoner av regningartene og Keplers tønneregel. Det hører også med til forventet kunnskap. Se listen under for utfyllende.
Tønneregelen er beskrevet her , og nede på denne siden er det forklaring på overgangene til de andre formene.
→ Keplers tønneregel.Nytt pr 18.09.
→ Forklaringer til oppgavene 19.9→ De klassiske problemene.
Mappeoppgave
- Frihåndstegning av to regulære mangekanter.
- Konstruksjon av 3 regulære mangekanter, deriblant femkanten.
- Frihåndstegning av omskreven og innskreven sirkel til en trekant.
- Konstruksjon av omskreven og innskreven sirkel.
- Skriv opp de geometriske stedene.
- Konstruksjon av to oppgaver (en trekant og en firkant) der Thales setning og Applollonius sirkel blant annet inngår.
- Konsture et utvalg av oppgavene over i geogebra.
- Finne tvillingtallene til fire tall, og vise at summen og kvadratsummen blir den samme. Vise at også kryssproduktene blir de samme.
- Bruke tvillingtall til å finne areal av en trekant.(Herons metode)
- Hvordan vi kan konstruere de ulike regningartene.
- Gjøre rede for Keplers tønneregel, og vise hvordan volumene for sylinder, kule og kjegle kan utvikles fra denne regelen.
Kunnskap
- Kunne konstruere regulære mangekanter.
- Vite hva de ulike geometriske stedene innebærer.
- Kunne konstruere trekanter og firkanter der en bruker de ulike geometriske stedene.
- Kunne konstruere enkel oppgaver i geogebra
- Kunne lage oppgaver der de geometriske stedene blir brukt.
- Kunne regne ut arealet av en trekant ved hjelp av tvillingtall.
- Kunne konstruere regningsartene.
- Kunne Keplers tønneregel og bruk av denne.
- Kunne bevise noen setninger.
- Summen av vinklene i en trekant.
- Thales setning.
- Periferivinkelsetningen.
- 60 graders vinkel.