AbeLie matematikk

Figurtall og tallmønster

---

Begreper

• Figurtall
• Tallmønster
• Trekanttall
• Firkanttall
• Teraedertall
• Kubetall
• Pascals trekant

---

Figurtall kaller man slike tall som oppstår av antall elementer i figurer. Tallmønster er følgen av slike tall. Vi ser på trekanttall, pyrmidetall, firkanttall og kubetall

Trekanttallene
De enkleste figurtallene er trekanttallene. 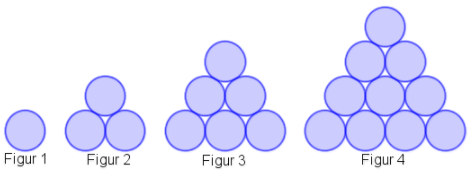De fremkommer ved å sette elementer slik at de danner en trekant. Det blir det samme som å legge sammen et visst antall naturlige tall. De fire første trekanttallene blir da $T_1=1, T_2 = 3, T_3 = 6$ og $T_4 = 10$.
Den generelle formelen for trekantallene er $$T_n=\frac{n(n+1)}{2}$$ Visuelt bevis for formelen: Induksjonsbevis for formelen. $$\frac{n(n+1)}{2}-\frac{(n-1)(n)}{2}=n$$ Alle perfekte tall er trekanttall.
Tetraedertallene
Summen av trekantallene gir tetraedertallene. Vi kan se dem som om vi legger trekantall oppå hverandre. Formelen for disse er $$T_n=\frac{n(n+1)(n+2)}{6}$$Dette er også formelen for summen av et visst antall trekantall.

Firkanttallene
De neste tallene er firkanttallene, eller kvadrattallene som de vanligvis heter. Som sagt oppstår trekantatallene ved å legge sammen de naturlige tallene. Firkanttallene kan fremkomme som summen av oddetallene.

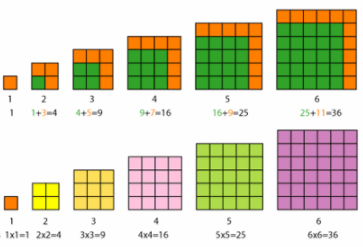
Formelen for summen av firkanttallene er gitt ved $$F_n=\frac{n(n+1)(2n+1)}{6}$$
Kubetallene
Kubetallene er de tallene som oppstår av antall elementer i en kube. De er gitt ved $$K_n=n^3$$Summen av kubetallene finnes enkelt som det tilsvarende trekanttal i andre: $$\sum K_n=T_n^2$$
Pascals trekant
Et setralt tallmønster som dukker opp i mange sammenhenger er det man kaller Pascals trekant. Den fremkommer ved en prosess der man starter med et ettall i første rad. I andre rad setter man et ettall på hver side av det som er over. I tredje rad vil vi ha tre tall. De to første er to ettall som står på hver sin side. Mellom disse står 2, som er summen av de to etttallene over. I neste rad finnes 4 tall, også her to ettall på hver side, og mellom disse summene av de over, så tallene her blir 3 og 3. Og slik fortsetter det ndeover.

Summen av hver rad er en toerpotens.

Vi finner de naturlige tall i en rad på skrå nedover.

I en rad ved siden av denne finner vi trekanttallene, og i neste rad finnes tetraedertallene.

Passcals trekant oppstår også når vi løser opp potenser av binomer.

• $(a+b)^0=1$
• $(a+b)^1=a+b$
• $(a+b)^2=a^2+2 a b+b^2$
• $(a+b)^3=a^3+3a^2 b+3 a b^2+b^3$

Sage computer

---