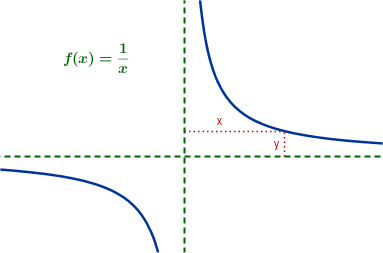
Disse funksjonene er en enkel brøk med x i nevneren. Man kan også si at produktet av f(x) og x er konstant.
Disse funksjonene har lineære funksjoner i teller og nevner. Det generelle utrykket er gitt ved: $$f(x)=\frac{a x+b}{c x+d}$$Funkjonen har et nullpunkt som man finner ved å sette telleren lik 0, og så finne x.
Videre har den to grenseverdier. Den ene grenseverdien har vi når nevneren er lik 0, da har vi ikke definert noen verdi for f(x), men f(x) nærmer seg uendelig når x nærmer seg denne verdien.